Python on Modules up on Github

Well the title is self-explanatory. Link here:

https://github.com/NanoSmasher/prob-cfvg

This link can also be accessed from the Research tab. First thing is that, unless you’ve got a geniuses mind you’ll have no idea what to do. Even if you have done python. I’ve only gone through rudimentary cleaning and commenting, which is to say; very bad programming practice. Hopefully given a bit of spare time I’ll make a pseudo-interface and maybe a GUI eventually.

Setup

For the absolute beginner:

  1. Download and Install Portable Python 3.x (I’m using 3.2.5.1 but any other extension should work). It has the IDE set up and everything, so you don’t have to hassle over setting up the interpreter and PATH.
  2. Either download each file from my github page separately OR hit the button on the right that says download zip to download them all. You know what to do with zips.
  3. Open up PyScripter-Portable.exe in whatever folder you installed Portable Python in.
  4. File > Open and search for any of the .py files that you acquired from (2)
  5. Hit Run (Shortcut: Crtl+F9)
  6. If you don’t see any warning or red popping up you are good to go!
  7. Move cursor/caret to the python interpreter at the bottom.

So once you have whatever file you have running, there are special commands you can type. For convenience I have italicized and bulleted it . Following this setup, just type in function(arg), where function is the italic part in the list and arg is the arguments or numbers you put in. Here is an example function.

  • quickodds(a,b,c,d)

Will be shown like this once you hit [Enter]:

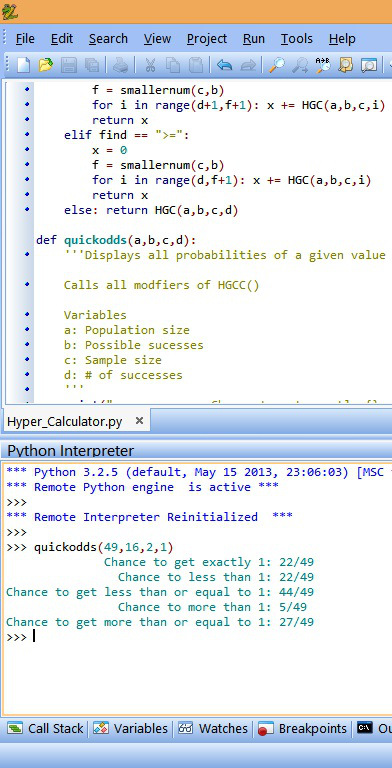
Example interface

Pay attention to make sure the command you type is the same character by character (this includes capitals). Also be careful with your arguments.

Modules

So let’s look at the files I have so far:

Hyper_Calculator.py

Note: Almost nothing else will work if you don’t have this one file!

This file does ALL the heavy lifting. It sports all the probability modules. Things like permutations, combinations, and a function for calculating the hyper-geometric cumulative distribution calculator. Using the Fraction class makes things neat and very precise. You can still use this module for fun with two commands:

  • quickodds(a,b,c,d)

a: Population size OR number of cards in the deck
b: Possible successes OR number of specific cards you want to pull in the deck
c: Sample size OR number of cards to draw in a row from the current deck
d: # of successes OR number of cards drawn that are those specific cards you wanted

Gives the same result as if you used stattrek’s calculator

  • cascadeodds(a,b,c)

Using the same parameters/arguments as quickodds. This simply print the odds for every possible /d/ value.

Quintetwall.py

Type in

  • foo()

Get back average percentage of getting a certain value of shield.
*foo() has no arguments

Ride.py

Excluding Generation II (Tsukuyomi, Galahad) this prints probabilities of getting up to grade 3 in three turns based on the input.

  • ChanceToGetMin1(ini,end,n,mull,first)

This is a masterpiece of pain. The module uses this function extensively. Note that you can skip the latter 2 arguments to save time: ChanceToGetMin1(1,6,4) is the same as ChanceToGetMin1(1,6,4,3,True). Rest of the documentation will appear if you type the function in.

Q: Why am I getting fractions?A: Cause it is accurate. I’m pretty sure you’ll learn how to use the print() command.

  • BasicRide(gr1,gr2,gr3)
  • AdvanceRide(gr1,gr2,gr3,gr4)
  • Gen1Ride(g1,g2,g3)
  • Gen4Ride(g1,g2,g3)
  • Gen2Ride(gr1,gr2,gr3,r)

All but this one expects you to have 4 of each copy already in the deck. This one though, take /r/ as the number of the grade one ride piece. I was doing calculations with this number but it was quite useless later. you can omit r altogether and it’ll treat is as 4 copies.

TriggerCompare.py

Incomplete.

Once done, it’ll be the first one written with documentation and cleaning done as I go along. It even has an interface. Therefore, I don’t have to tell you as much.

What does it do? Something quite a few people are wondering, proof for the best trigger ratio. This program compares the hand, shield and change in damage based on the trigger lineups specified by the user. 16 draw? 9S/5C/2H ? Now you are no longer bound to solid multiples of 4 and 6.

Conclusion

That’s all I have. I’ll upload and update more of the modules I have to do my research. Hopefully I can have transparent data available for peer review, modifications and the like. Whenever you doubt me, you can check the code and see how it works!

Hypergeometric Cumulative Probability Calculator

Recent Posts

Archive