Stride Probabilities

• Brampton Booster
• May 03, 2015
• Comment

In a year from now, anyone picking up vanguard for the first time would believe that Stride was a mechanic from the very beginning. Unlike other card games which shove in a mechanic for the sake of novelty, Bushiroad shows that when it wants to create good design they succeed very well.

Vanguard has always pushed for quality over quantity, by allowing each resource to be used in multiple ways¹. The Deck can be drawn and stacked, and the Drop Zone can aid in Legion. The Damage Zone was the most ingenious by having triggers, counter blasts, unflipped, limit breaks, card swapping, and card inclusions maximizing its utility. So the G-Zone had to be more then just an extra deck. This was a achieved by having it work in a reverse Damage Zone; cards are flipped face up and face up cards contributed to G-breaking/counting. This is why stride fits so well into the current game and honestly, should have been in the game at the very start.

But how has Stride changed the game we play today? Do the triple checks and card cycling push the game too far? Or has Vanguard’s Day 0 future-proofing technology shown us what it truly means to have brilliant game design?

G-Assist really works

Surprising nobody, G-Assist has fixed many complaints about being grade locked. But by how much did it really help? By calculating the difference with and without G-assist, basic ride success have been fixed by at least 14%. Below is the output of the results:

G Assisted	Normal	Difference	Grade 1	Grade 2	Grade 3
0.96495	0.82942	0.13553	12	11	10
0.96343	0.82595	0.13748	11	12	10
0.96302	0.82416	0.13885	11	11	11
0.96262	0.82629	0.13633	12	12	9
0.96205	0.82579	0.13626	13	11	9
0.96198	0.82306	0.13892	12	10	11
0.96183	0.82434	0.13748	13	10	10
0.95943	0.81937	0.14006	11	13	9
0.95847	0.8157	0.14277	10	12	11
0.95836	0.81433	0.14404	11	10	12

And the ranking without G-Assist

G Assisted	Normal	Difference	Grade 1	Grade 2	Grade 3
0.82942	0.96495	-0.13553	12	11	10
0.82629	0.96262	-0.13633	12	12	9
0.82595	0.96343	-0.13748	11	12	10
0.82579	0.96205	-0.13626	13	11	9
0.82434	0.96183	-0.13748	13	10	10
0.82416	0.96302	-0.13885	11	11	11
0.82306	0.96198	-0.13892	12	10	11
0.81937	0.95943	-0.14006	11	13	9
0.8157	0.95847	-0.14277	10	12	11
0.81433	0.95836	-0.14404	11	10	12

An important fact is that the top grade ratios are different whether you compare by G-Assist or not. Nonetheless, The best grade ratio is the same for both tables. By ranking the G-Assist changes the ranking like this: 1, 3, 6, 2, 4, 7, 5, 8, 9, 10².

We can compare it to the best ride chain (Stern) to see improvements in that:

G Assisted	Normal	Difference	Grade 1	Grade 2	Grade 3
0.97029	0.8594	0.11089	13	10	10
0.97008	0.86256	0.10752	13	9	11
0.96962	0.85748	0.11215	12	10	11
0.9691	0.8612	0.1079	14	9	10
0.96822	0.85188	0.11633	12	11	10
0.96781	0.8572	0.11061	12	9	12
0.96664	0.85318	0.11346	14	10	9
0.96648	0.86118	0.1053	14	8	11
0.96621	0.84895	0.11725	13	11	9
0.96588	0.85912	0.10676	13	8	12

Difference is smaller as expected. Ranking for type one ride chain 13+ grade 3’s looks like this:

Normal	G Assisted	Difference	Grade 1	Grade 2	Grade 3
0.85147	0.96274	-0.11127	12	8	13
0.84937	0.95735	-0.10798	13	7	13
0.84551	0.96233	-0.11681	11	9	13
0.84037	0.95386	-0.11349	12	7	14
0.83842	0.95688	-0.11846	11	8	14
0.83151	0.95633	-0.12482	10	10	13
0.82755	0.95321	-0.12566	10	9	14
0.82672	0.948	-0.12128	11	7	15
0.81984	0.94772	-0.12788	10	8	15
0.80922	0.94436	-0.13514	9	11	13

One needs to remember the cost of G-Assist though. A minus 1 in the early game can be fatal against certain decks. While you can go with a ridiculous 4-1-28³ with a 75% success rate it will cost you severely since you will G-Assist more then half the time. Since I can not phantom any Morikawa-type deck that requires such a ridiculous ratio (and a severe lack of grade 1 boosters), it would be much safer to stick with the pre-stride era rankings.

Stride increased cycle speed

There is a nice rule of thumb when checking how often a card would show up; by having it divided by the deck size.

• Perfect guards happen every 12 cards (49/4 ~= 12)
• Having a main[4] and backup[4] set keeps a cycle at 6 cards (49/8 ~= 6)
• Triggers will appear every 3 cards (49/16 ~= 3)

And there are two cycles pre-stride; the Mulligan and turn 3 onwards. The base tempo is 3 cards, one for drawing and another two with twin drive. It is expected to go through 1 other card by damage, and usually one more by advantage decks (RP,OTT,NN) making tempo around 4.5. The starting, Mulligan, and first draw goes through 9 cards which is double that. In the first couple of turns or past turn 7, tempo is only 2-3. From this data you can tell perfect guards are picked up every three turns while triggers pop up every single turn. However, there is a smaller chance to have a trigger activate in the right timing (2/4.5) while important cards have better odds (4/4.5). As the cycle normally continues about 5 times you can see how nicely the numbers line up.

When Stride came in vanguard suddenly became much faster. Although the beginning is still 9 cards, an average turn of striding is now 6. You draw, then triple check, G-skills activate, and you very often take damage. Triggers now have a 12% increase to (3/6) and key cards show up (5/6). This means perfect guards now move from every three turns to every two turns, and you get two triggers every cycle. So if you considered why stride had obvious power creep that didn’t seem to translate completely, it’s due to additional speed created in picking up defensive cards. However, that isn’t enough…

Heals are useless, 16 CRIT all the way

Before you label me as a lunatic please consider the data I have gathered on this. When I say heals are useless, I’m referring to a specific situation where both players are using vanguard with triple drive from turn 3 onwards. I mean, there is no such thing as a triple checking vanguard right?

Sarcasm aside, nobody is going to Stride for 6 turns straight. Whether it be by choice or by restriction (Too much G-flipping or can’t discard a grade 3) players will attack with grade 3’s. Now, as most of the decent finishers are either re-standing vanguards or pg-nullifying units heal triggers are both extremely valuable and a major hindrance. While the meta leans toward 12 CRIT, if Striding becomes cheaper and Strides become stronger the game might inherently move towards 16 CRIT⁴.

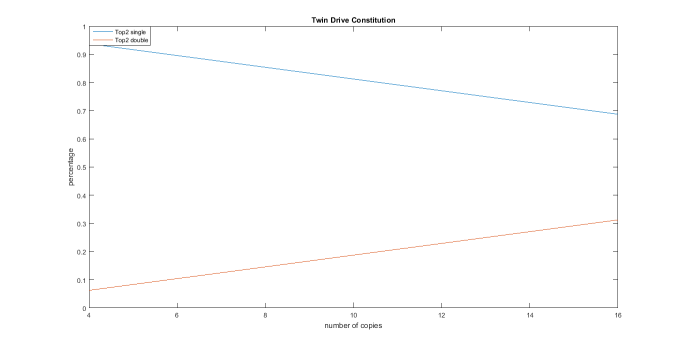
So, let’s assume this futuristic world then and map out probabilities for getting a crit in twin and triple drive:

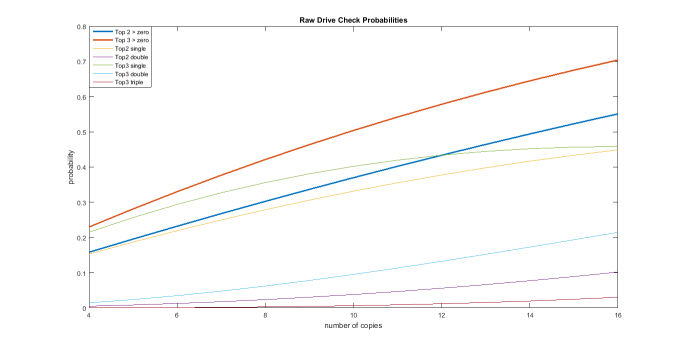
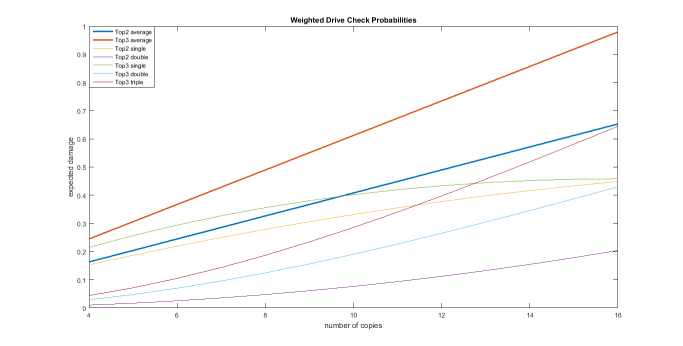
First of all none of these lines have a linear relationship but rather a hypergeometric one. This is a generic graph where we will base everything on. While it be for perfect guards or grade 3 the probabilities are the same meaning this chart can be used for further analysis. We are focusing on critical triggers for this article; The bold blue line is the chance of getting at least one crit in twin drive (referred to as /#/2 from now on) while the bold red one is for triple checks (/#/3). The lines may have the same shape but /#/3 has a slightly higher slope edging out at 0.7 while /#/2 is down at 0.55. This should be obvious as we are comparing twin drive to a triple drive. But these lines do not show to average amount of extra damage dealt per drive check. Getting two critical triggers mean 2 extra damage and three makes 3. So we need to weigh each probability to match the expected damage output which is reflected in Figure 2:

As calculated before, running 12 critical triggers increases the damage tempo from 1 to 1.5 per turn, having 8 is a 1 -> 1.33 and 16 is 1-> 1.66. One interesting fact is that /#/2’s drive tempo is linear meaning that triggers are in fact separated by ratios (1 + 0.5/12*8 = 1.3). This is also true for the triple check and as you can already see, it has an absolute dominance over everything. So if there is 16 critical triggers in your deck, the tempo of /16/3 is 2 damage per turn. Due to the linear relationship it means that 16 crit increases damage at twice the rate of 8 crits.

If you read through this argument a couple of times, you might realize that since tempo of /#/2 is also linear, the double tempo thing applies to /16/2 as well. But you fail to account two things:

1. 16 critical triggers do not increase true tempo to two damage per turn, and
2. Heal triggers exist to mitigate the damage dealt by extra critical values

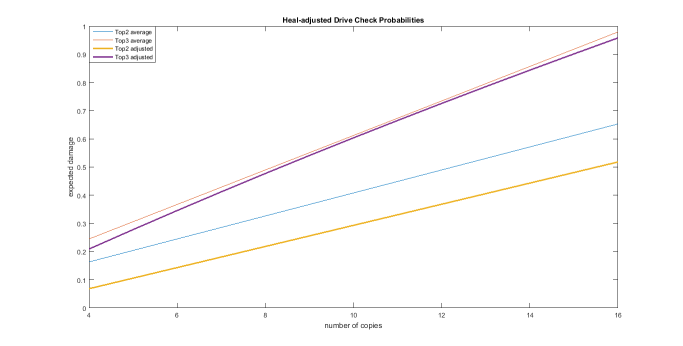
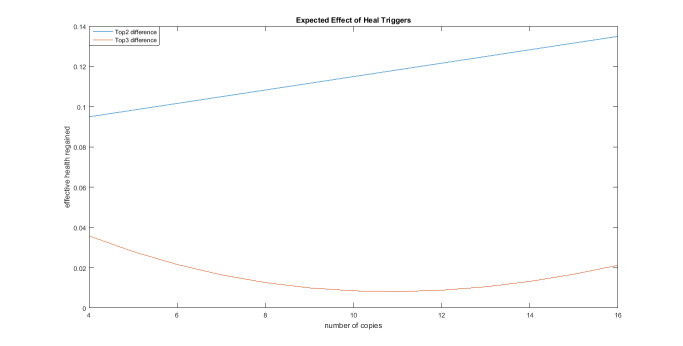
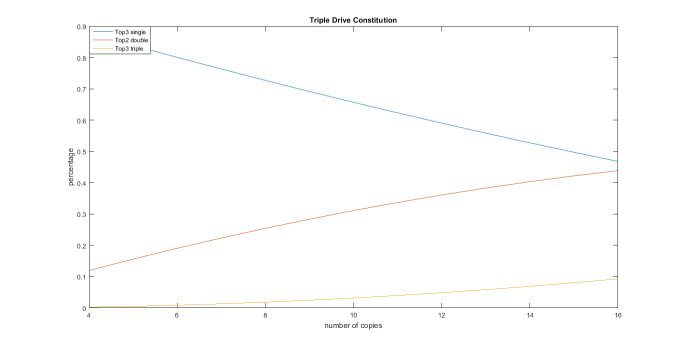
This is my strongest case for 16 crits. Look at the difference between /#/2 /#/2+adjusted. The difference is more then 10%. But between /#/3 and /#/3+ there is next to no difference. Figure 4 below calculates the actual difference and blows it up to make it easier to see. In //twin+, as you put more and more crits in your deck, the stronger the effect of heal triggers becomes. But this is not the case for /#/3+. In fact, the effect of heal triggers get weaker as you put more crits until you hit 12 copies. This concludes that /#/3 practically makes heal useless, which is what all my research has lead me.

It does not matter what number of criticals you use in your deck, Striding basically has a hidden CONT that screws over your opponent’s heals⁵. At the low end /4/3+ is 250% more effective then /4/2 while the other end /16/3 is 700% more effective then /16/2. Combined with strong linear slope /16/3 has you can force the game to move twice as fast and kill threaten death even at a normal 3 damage. But there is something more unsettling when drive composition comes into play.

We first show a deconstruction of the twin drive. As you can see it’s quite tame. You are more likely to get a single crit then two regardless of how many triggers you put in. Even at 16 copies, double crit only happens a third of the time. The actual probability to get it is actually one half of one third of two thirds, or 10%. When I mean a third, I mean the composition tells me that if I do get a crit on the first check I have a one in three chance for the other trigger to be a crit.

Nothing about the figure is particularly interesting, except at the very end. By extrapolating the number of triggers by one the lines actually cross and hence a higher chance of getting two criticals as opposed to just one. So let’s take in account 16 critical triggers again: In twin drive, a crit on the first check signifies a 33% for a second one. But in triple drive getting a crit on the first check implies a 55% chance to pick up another⁶! (Don’t forget the chance of a triple crit).

In terms of raw probabilities you are still going to miss getting a trigger 30% of the time. And if they guard for two to pass, it will still benefit them 60% of the time (Though for twin drive it works 90%). But be aware of your situation; if you get a crit and the guard wasn’t perfect you have a great chance to take them out right there.

Sticking with heals

To reiterate; If the meta changes over to triple checking vanguards 16 crit will be more effective then any other ratio. /16/3+ will force a damage tempo of 2, negate the power of heals, and has a high chance to break two-to-pass defending. If the opponent can not defend they get an average of two damage dealt: obviously this is accounting the weight of double and triple crits. They only get perfect guards one in three turns [HGCC(49,4,4,0,”>”)], and in this case the best decks will be pumping power so a rearguard can also swing for 5+ stages and 2+ crit (ideally). Speed is your friend: you want to keep both parties invested in Stride so you can reap all the benefits.

However twin drive is still a central part of vanguard and it isn’t going to leave peacefully. Breakrides and limit break decks in general now have a response to their stagnated mid-game power, while Legion finds another way to drop cards at a faster rate and protect it while the drop zone builds. Restanding vanguards that plus generously are still limited to twin drive, and of course the G-zone does have a set limit of 8. Lastly, stride requires a blood sacrifice and not every deck can provide them with a limitless of grade 3’s. When the fuel supply runs out, so is the advantage of /16/3.

Figure 4 (The one on expected effect of heals) wrap up the benefits of staying loyal to 12 Crit/4 Heal. If the opponent opts for /#/2+ you will have to tank the 0.33-0.5 damage tempo instead of the greatly reduced 0.22-0.4 pacing that you have been used to beforehand. And when combining both twin and triple drive, 12 crit fit right into the minimum of that curve while having a medium effect on heals. In symbolic terms, /#/2 > /#/3 for you <=> the opponent is /#/2.

Protection

I’ll close out with how effective future-proofing has done for vanguard. Stride is definitely a game-changing mechanic that causes us to re-evaluate a lot of different decks and situations that was often bad or marginal. It benefits every deck and improves consistency. Disregarding the ability to solve grade locking, the consistency has the added benefit of increasing tempo both offensively and defensively. While offense gets the better deal, there is still enough room to wriggle out of tight spots. Unfortunately the game is very close to tipping over to one side, so Buishiroad will need to find a way to improve a defenders turn before power levels become too high to defend properly. With my midgame standard form being less accurate I will lean towards early game optimization. Keep a good eye out so you can see if the metagame shifts to a /16/3 favoured build before the next game-changing mechanic arrives.

---